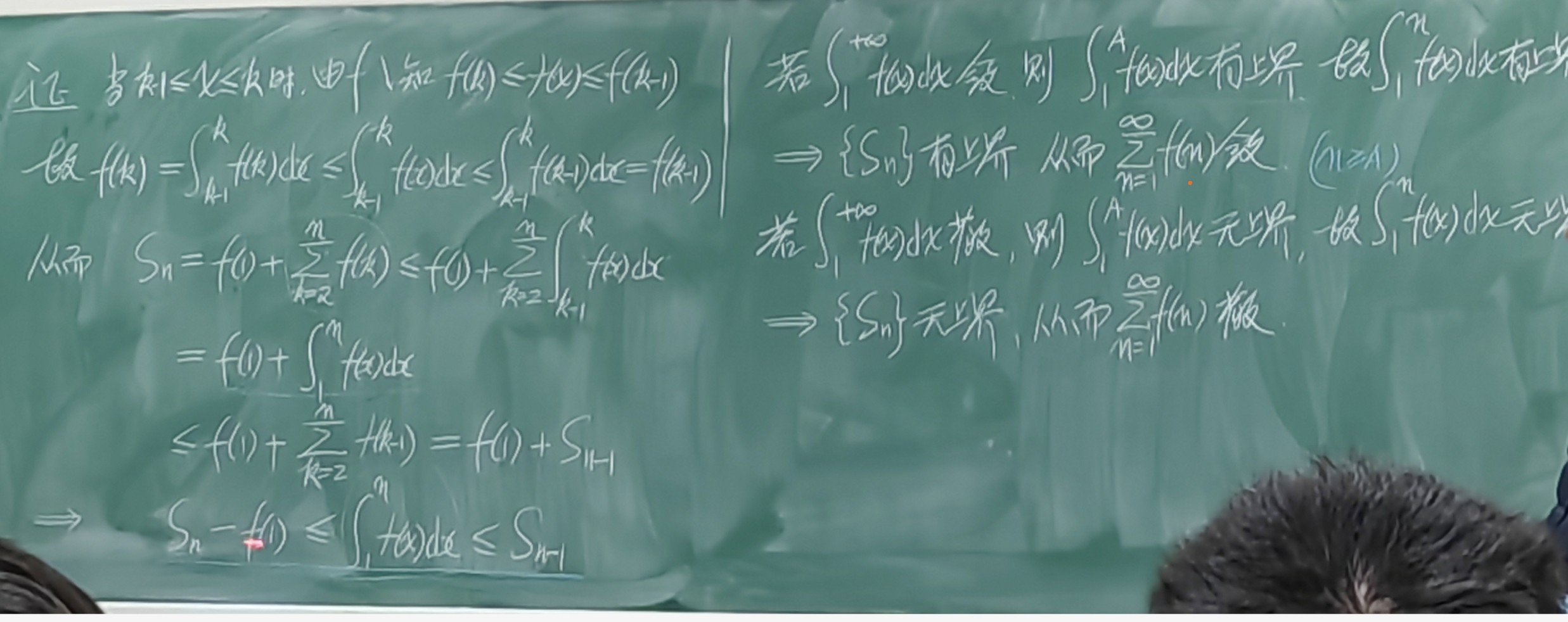或
Chap 7-1
数项级数
一、基本概念与性质
flowchart LR
subgraph 性质
级数 --- 更改有限项敛散性不变
级数 --- 收敛线性性
级数 --- 收敛的结合性
级数 --- 更序级数敛散性不变
end
subgraph 简单级数
级数 -- 必要条件 --> 通项极限为0即收敛 <--> 极限不为0/不存在即发散
级数 --> Cauchy收敛/发散准则 --- 放缩
end
subgraph 正项级数
级数 --> 收敛原理 --- 部分和有上界
级数 --> 比较判别法 --- A["大收➡️小收\n小散➡️大散"]
A --> 极限形式
A --> p-判别法
级数 --> B[根值判别] --- B1[≤q<1 收敛]
B --- B2[≥1 发散]
B --- B3[=q == 1?]
级数 --> C[比值判别] --- B1
C --- B2
C --- B3
C --- 双比值
级数 --> D["积分判别\n1~∞"]
C -.-> Rabbe判别法 --- E["α ↔1"]
end
subgraph 一般级数
subgraph 交错级数
级数 --> Leibniz --- 单减有界
end
级数 -.- Riemann重排
级数 -.- Abel变换
级数 -.- Abel引理
级数 --> A-D判别法
end
设 是一个数列, 则 #级数/形式和(形式上连加)
称为 无穷级数 (简称 #级数 ), 和式中的每一项称为级数的项, 称为级数的通项(或一般项), 而
称为级数的前 项 #级数/部分和
若 , 则称级数 收敛, 且收敛于 称为级数的和; 记为
若 发散, 则称级数 发散
- 此处是形式和,只是一种记号
- 级数的敛散性通过 (部分和)的敛散性规定
若 , 也称 发散到
例1 讨论 #几何级数 (通项为等比)
的收敛性
Solution
结论:几何级数当且仅当 收敛
且和为 前项公比
Cauchy收敛准则
收敛
Cauchy发散准则
发散
Proof
取取
敛散性不变
Analysis
有限项->存在最大下标->存在n大于最大下标
即可用于:n充分大的条件
基本性质
线性性
若级数 , 则级数
若 发散, 问 敛散性如何?
不一定
若 收敛, 发散, 则 敛散性呢?
发散
必要条件
若级数 收敛, 则
Proof
设: , 部分和为 , 则
逆否命题成立: 或不存在 发散
逆命题不成立: 不一定能导出 收敛/发散 Eg.调和级数
例3 判断级数 的敛散性
Solution
故发散
二、正项级数的敛散性及判别法
若级数 满足 , 则称之为正项级数
显然,正项级数的部分和 单调增加, 因此有
收敛原理
设 , 则
收敛部分和有上界
注
要么收敛要么发散到正无穷
- 若 有上界, 则
- 若 无上界, 则
补充:结合律、交换律
结合律
若 , 将其相邻若干项加括号得到的新级数收敛,且和不变
Proof
设 部分和为 , 加括昂极限为
记其前n项和为
则
由于
故由归并性:
发散 , 但 收敛
定理: 更序级数敛散不变
设 , 则任意更换顺序求和所得新级数敛散性不变, 收敛时和不变.
Proof
设 ,部分和
且 是 更序级数
中的项均来自于
设 : 在原级数中最大下标为
则 中的某些项
有上界
从而 收敛
且其和:
又 可视为 的更序
故
同理 正项级数若发散,更序级数亦发散
例题
Proof
有上界故原级数收敛
Solution
当 时
由于 发散, 故 无上界故 无上界
发散当 时

设: 从而
负数故 有上界,原级数收敛
比较判别法
若 与 为正项级数, 且 ,则有
收敛收敛发散发散
Proof

Proof
由于 且 发散
由比较判别法: 发散
推论 (极限形式)
设 , 且 , 则
- 当 时, 与 同敛散
- 当 时, 收敛 收敛
- 当 时, 发散 发散
Proof
(1)详细证明如下
由
取 , 则 则
若 收敛 收敛
若 发散 发散
小散 大散: 发散
(2) => 大
(3)同理
说明
- 常选择几何级数与 级数作参照级数
- 常估计通项无穷小 对 的阶
^10fi2j
设 , 且 , 则
- 当 , 且 时, 收敛;
- 当 , 且 时, 发散
- 理解:
- 说明 发散到 ,若此时还能让 不发散到 ,则一定是一个收敛的数列将其拉回来
- 说明 收敛到 ,若此时还能让 不趋近于 ,则一定是一个发散的数列让他拉起来
Analysis
证明即为之前极限形式的特例
例7 判断 的敛散性
Solution
由于 (等价无穷大)且
故原级数收敛
Solution
由于且故原级数收敛
Tips
Cauchy判别法 / 根值判别
若正项级数 满足
- , 则 收敛
- 有无穷多项使 , 则 发散
- , 则
- 当 时, 收敛;
- 当 时, 发散;
- 当 时, 判别法失效
Proof
(1) 由条件: 且 收敛
比判 收敛
(2) 由条件:
故 从而 收敛
(3) 当 时
由不等式性: 有
由(2): 收敛
当 时
, 有
当 时
发散,
再考虑
例9 证明 发散
Proof
根据Cauchy:发散
d'Alembert判别法 / 比值判别法
若正项级数 满足
- , 则 收敛
- , 则 发散
- , 则
- 当 时, 收敛;
- 当 时, 发散;
- 当 时, 判别法失效
Proof
(1)由条件:
且 收敛
故 收敛
(2)由条件:
知:
(3)...
例10 讨论 的敛散性
Proof
(1) 时: 收敛
(2) 时: 发散
(3) 时:
原式由比值法 (2): 发散
积分判别法
若非负函数 在 上单减, 则级数

Proof
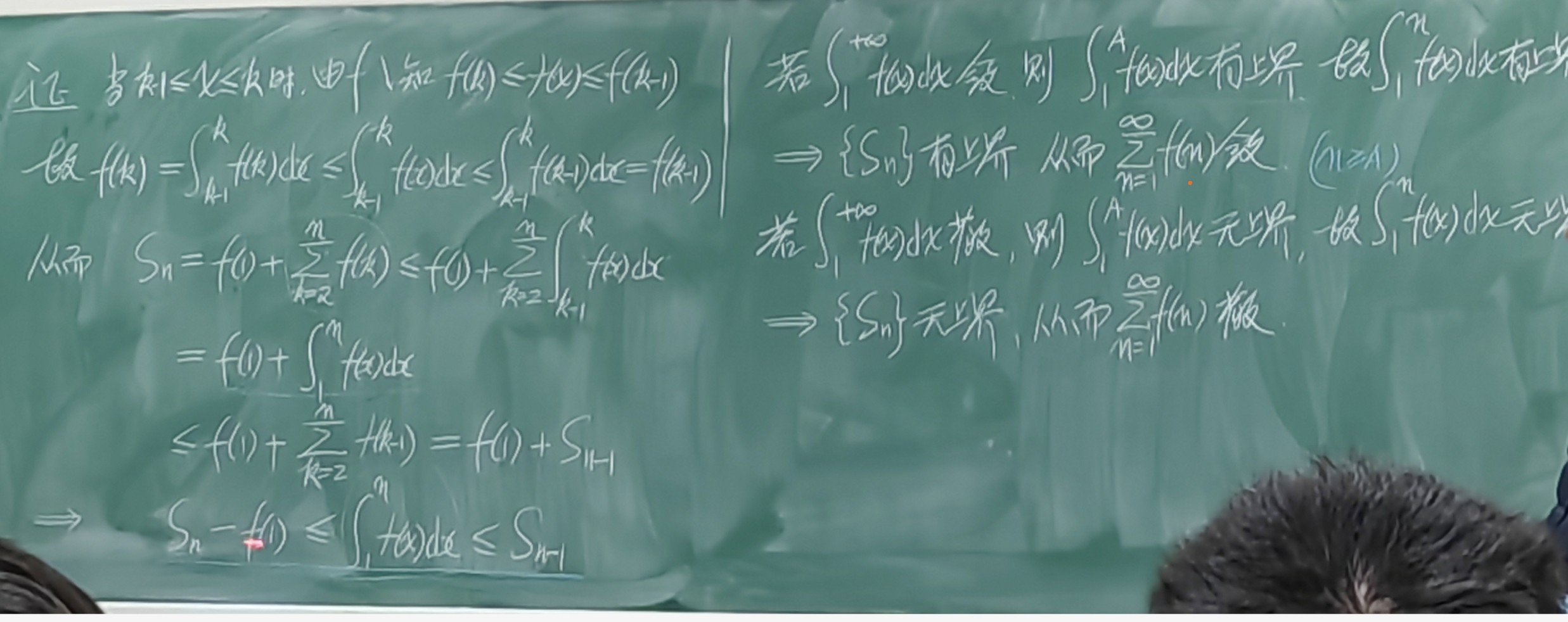
例11 讨论 的敛散性
Solution
则 非负递减,且
Note: 时发散
补充:比值判别法2
设 ,且
则
- 收敛 收敛
- 发散 发散
Proof
叠乘:
再由比判可证
Raabe 判别法
设 , 且
若 , 则 收敛; 若 , 则 发散
Proof
当 时,取
由不等式性:
比判二收敛当 时
比判二发散
例12 设 , 讨论超几何级数
的敛散性
Solution
故
当 时, 原级数收敛
当 时, 原级数发散
当 时, 考虑 #Raabe判别法
故
从而当 即 时,原级数收敛
当 时原级数发散
当 时,运用高斯判别法
三、一般级数的收敛性及判别法
交错级数
正负项相间的级数称为 #交错级数, 其形式为
或其中
Leibniz 判别法
若交错级数 满足
则 收敛, 且
Proof
设即 单增, 且
即 有上界
故 收敛,记 且
又从而
绝对收敛/条件收敛
若 收敛, 则称 #绝对收敛
若 收敛, 而 发散, 则称 #条件收敛
若 收敛, 则级数 收敛
Proof
由 收敛 Cauchy 准则
传递性
若 绝对收敛, 条件收敛, 问
是绝对收敛还是条件收敛? 为什么?
条件收敛
Proof
收敛, 收敛
线性 收敛
由 ,
其中 收敛, 发散
发散
进而 发散
比判 发散
条条 条/绝
例13 判断 的敛散性.
Analysis
申必的交错级数
Solution
非常隐秘的交错级数!
其中: 判 原级数收敛
又 调和 发散
发散
原级数条件收敛
判断 若 , 则 与 同收敛
错误
反例:
令则
但 发散,
收敛(L-判)
正部、负部
设有一般级数 , 称
和为 的正部和负部.
- 负部大于0
Eg.
此时
由此可得到
若 绝对收敛, 则 和 都收敛;
若 条件收敛, 则 和 都发散至 .
1)
因收敛
比判收敛
2)
条件收敛
收敛,
线性
收敛级数的交换律
例14 已知 , 考虑级数
(更序)
证明:
证:设 ,而 前 项和为
由于规律, 考虑3 个一组, 则
又
设 绝对收敛, 则任意改变求和顺序所得新级数也绝对收敛, 且和不变.
Proof
设
更序级数 , 则有
注: 例如:
由于
故 收敛
且
Riemann 重排定理
设 条件收敛, 则对 存在改变求和顺序的新级数使之趋于
Abel 变换 / 分部求和公式
设有 , 记 , 则
Proof
记则又
Abel 引理
设 单调, 若 , 则
Proof
由分部求和公式得
单调
A-D判别法
设 , 满足下两条件之一: 则 收敛.
(Abel) 单调有界, 收敛;
(Dirichlet) 单调趋于 的部分和有界.
Analysis
单调其中Proof
设 又 收敛知:
故
Tips
#数项级数/三角凑项
Proof
今则且令证明 收敛: 积化和差
凑项倍公差的一半故 判 收敛
其次
调和发散乘故 发散
判 发散
条件收敛
Solution
当 时,原级数为调和级数: 发散
当 时
令且Addition
若讨论是否条件收敛:
四、级数的乘积
熟知
是否想等存疑更序后结果可能不同因此写成数阵:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cauchy 乘积
记 , 则称 为 和 的对角线乘积(或 Cauchy 乘积)
例17 考察 与自己的 Cauchy 乘积
Analysis
根号趋于0:L-判
通项加绝对值:发散 ()
Solution
发散
两个条收 收
Mertens 定理
设 且至少其一绝对收敛, 则它们的Cauchy乘积收敛, 且
Analysis
且,则上三角元素加完有限交换按行加下标大:收敛小小下标大小小的界Proof
先证 的情形
即 故可设
,由 收敛: , 有
又 对上述 , 有
令 , 有 , 故
再证 的情形:
令 则
例18 已知 , 令
(1) 证明:
(2) 求极限:
Solution
(1) 令 且
故
为 的部分和
Cn为C乘积部分和
(2) 由、有:
故原极限
或令Abel 定理
设 . 若它们的 Cauchy 乘积收敛, 且 , 则
Solution
由于
从而: 画出数阵
同除n:
例五、无穷乘积*
设有非零数列 , 称
为无穷乘积. 记部分乘积
- 若 , 则称无穷乘积收敛, 否则称其发散
若 收敛, 则有
无穷乘积 收敛 收敛.
Proof
则即若则若则